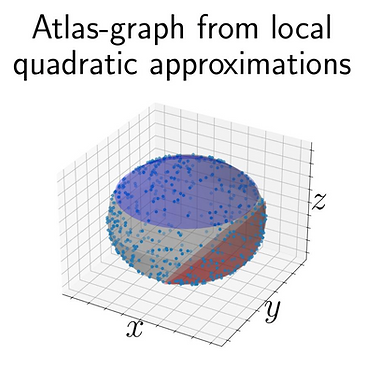
NITMB faculty member Samantha Riesenfeld, in collaboration with NITMB-funded PhD student Ryan Robinett and UChicago assistant professor Lorenzo Orecchia, have developed a new technique for learning and representing Riemannian manifolds that, unlike state-of-the-art dimensionality reduction techniques, preserves geometric and topological invariants and enables faster, more broadly applicable Riemannian optimization. In machine learning, Riemannian manifolds offer a useful abstraction for approximating commonly encountered, non-Euclidean empirical data distributions and optimization state spaces, including biological data. While Euclidean machine learning algorithms have been adapted to Riemannian manifolds, these adaptations rely on computationally intensive differential-geometric primitives, such as exponential maps and parallel transports. Riesenfeld et al. describe a novel numerical data structure, the atlas graph, that encodes a Riemannian manifold in memory using a finite set of overlapping coordinate charts, leveraging the fact that compact manifolds almost always admit such a set. Their theoretical and empirical work demonstrates that the atlas graph preserves several manifold invariants, such as homology groups, pairwise geodesic distances, and pointwise scalar curvature, which are not maintained by state-of-the-art dimensionality reduction techniques. First, they show a runtime advantage of this framework for first-order optimization in a setting where the manifold is expressed in closed form, i.e., over the Grassmann manifold. Furthermore, using high-contrast image point cloud data, for which a nontrivial manifold structure was previously established, they show that an atlas graph with the correct geometry can be directly learned from the point cloud. Finally, they demonstrate that learning an atlas graph enables downstream key machine learning tasks, such as a Riemannian generalization of support vector machines, that uses the learned atlas graph to approximate complicated differential-geometric primitives, including Riemannian logarithms and vector transports. These settings suggest the potential of this framework for even more complex, biological settings, such as in RNA-sequencing data where ambient dimension and noise levels may be much higher, which Riesenfeld et al. are currently exploring. Taken together, their results speed up and render more broadly applicable Riemannian optimization routines at the forefront of modern data science and machine learning.